Unit 2.1 - Demand, Supply and Market Equilibrium - Numerical Illustrations

1. If autonomous demand is 12 and slope of demand curve is 2. Find the demand function.

Solution:

Given,     Autonomous demand (a) = 12
                Slope of demand curve (b) = 2
We know that,
                Q_d = a – b p
                Q_d = 12 – 2p is the required demand function

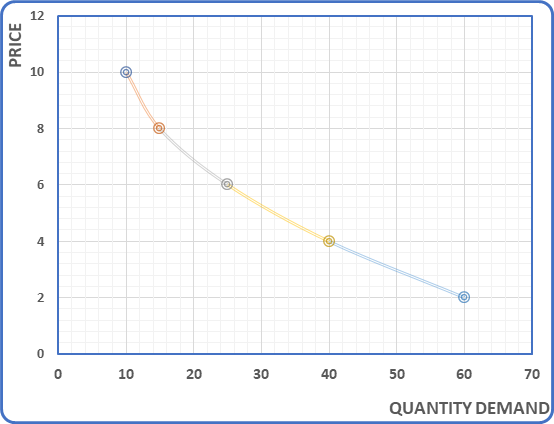
2. From the following demand schedule for commodity X, draw the demand curve, what type of demand function does it represent?

Price (Rs./Kg.)	10	8	6	4	2
Quantity (Kg./month)	10	15	25	40	60

Solution:

In the above figure, DD is a demand curve derived on the basis of given demand schedule. It represents non-linear demand function.

3. The following table shows the amount of rice bought by a household at different prices and time period.

Period	Price per Kg.	Amount Bought
January, 2001 January, 2005 January, 2010	Rs. 25 Rs. 40 Rs. 60	10 Kg. 35 Kg. 50 kg.

Does the behavior of the household contradict the law of demand? Give reasons for your answer.

Solution:

The law of demand states the inverse relationship between price and quantity demanded of a commodity but the above table shows positive relationship between price of rice and its quantity demanded. Hence, the behavior of the household contradicts the law of demand.

4. Suppose there are 100 identical individuals in the market for commodity X, each with a demand function given by Q^d_x = 5 – P_x. Derive market demand function, market demand schedule, and market demand curve at the given prices Rs. 0 to Rs. 5.

Solution:

Given, The individual demand function, Q^d_x = 5 – P_x
Market demand function for 100 identical individuals:
Q^d_xm = 100 × Q^d_x
or, Q^d_xm = 100 × (5 – P_x)
⸫ Q^d_xm =500  – 100P_x

Market demand schedule can be derived as follows:

Price in Rs.	Market Demand Qdxm =500  – 100Px
0 1 2 3 4 5	500  – 100×0 = 500 500  – 100×1 = 400 500  – 100×2 = 300 500  – 100×3 = 200 500  – 100×4 = 100 500  – 100×5 = 0

The derivation of market demand curve is shown in the following figure:

5. Derive the supply curve from the following supply function and say whether it is linear supply curve or non-linear supply curve.

Q^s_x = 4 + 2P_x

Solution: Let us suppose P_x = Rs. 0, 1, 2, 3, 4 and 5. Then,

Price (Px­­)	Quantity Supplies (Qsx) = 4 + 2Px
0 1 2 3 4 5	4 + 2×0 =4 4 + 2×1 =6 4 + 2×2 =8 4 + 2×3 =10 4 + 2×4 =12 4 + 2×5 =14

The above supply curve SS represents linear supply curve. This means the value of slope in the fixed supply curve SS remains same even if price and quantity supply change.

6. From the specific supply function Q^s_x = 10P_x, derive

(a) Supply schedule (b) Supply curve (c) What things have been kept constant in the given supply function? (d) What is the minimum price that this producer must be offered to induce start supply? (e) What is the nature of the supply curve?

Solution:

(a) To derive the supply schedule, 

let us suppose P_x = Rs. 0, 1, 2, 3, 4 and 5.

Price (in Rs.)	Quantity Supplies (Qdx) = 10Px
0 1 2 3 4 5	10×0   = 0 10×1   = 10 10×2   = 20 10×3   = 30 10×4   = 40 10×5   = 50

(b) The supply curve derived from the supply schedule is shown below:

(c) The other determinants except price such as technology, price of inputs, prices of related goods, goal of the firm etc. are kept constant.
(d) Any price above zero will induce the producer to start supply.
(e) The supply curve derived on the basis of supply schedule is straight line. Hence, it represents linear supply function.

7. Find the equilibrium price and quantity from the following demand and supply functions.

Q^d_x = 10000 (12 – 2P)              and        Q^s_x = 1000 (20P)

Solution:

Given, Q^d_x = 10000 (12 – 2P)   and         Q^s_x = 1000 (20P)

For market equilibrium: Q^d_x = Q^s_x

10000 (12 – 2P) = 1000 (20P)

or, 10 (12 – 2P) = (20P)

or, 120 – 20P = 20P

⸫ P = 3

Putting the value of P in demand and supply functions,

Q^d_x = 10000 (12 – 2P) = 10000 (12 - 2×3) = 10000 (6) = 60000

and Q^s_x = 1000 (20P) = 1000 (20×3) = 1000 (60) = 60000

Hence, equilibrium price is Rs. 3 and equilibrium quantity is 60,000 units.

8. From the demand function given as P = (Qd+20)/3 and supply function given as P = Qs/2, find out,

a. Equilibrium price,

b. Whether there is excess demand or excess supply at Rs. 2 and 5 and find out the quantity of excess demand and excess supply at these prices.

Solution:

a. Given, Demand function, P = (Qd+20)/3

or, 3P = – Q_d + 20
or, Q_d = 20 – 3P ………(i)
Supply function, P = Qs/2
or, Q_S = 2P
For equilibrium price: Q_d = Q_S
or, 20 – 3P = 2P
or, 5P = 20
⸫ P = 4
Hence, equilibrium price is Rs. 4

b. At price Rs. 2

Q_d = 20 – 3P = 20 - 3×2  = 14
Q_S = 2P = 2×2 = 4
At Price Rs. 2, demand is 14 units and supply is 4 units. Hence, it is the case of excess demand.
Excess demand = Q_d – Q_s =14 – 4 = 10 units
Again, at price Rs. 5
Q_d = 20 – 3P = 20 - 3×5  = 5
Q_s = 2P =2×5 = 10
At price Rs. 5, demand is 5 and supply is 10 units. This is the case of excess supply.
Excess supply = Q_s – Q_d = 10 – 5 = 5 units

9. Given the following demand and supply equations

Q^d_x = 100 – 5P_x   and        Q^s_x = 10 + 5P_x
(a) Graph the supply and demand equation and show the equilibrium price and quantity.
(b) Determine the equilibrium price and quantity.
(c) If demand increases to
    Q^d_x' = 200 – 5P_x
    Determine new equilibrium price and quantity.
(d) Explain when demand equation changes, what happens to equilibrium price and quantity.

Solution:

Given, Q^d_x = 100 – 5P_x      and         Q^s_x = 10 + 5P_x

(a) Demand and supply schedule

Price (in Rs.)	Quantity Demand Qdx = 100 – 5Px	Quantity Supply Qsx = 10 + 5Px
7 8 9 10 11	65 60 55 50 45	45 50 55 60 65

Plotting the values of above schedule in graph, we derive demand curve (DD) and supply curve (SS). On the basis of schedule and graph, equilibrium price (P_x) = 9 and equilibrium (Q) = 55.

(b) For equilibrium,

Q^d_x = Q^s_x
or, 100 – 5P_x = 10 + 5P_x
or, 10P_x = 90
⸫ P_x = 9
Putting P = 9 in demand and supply equations,
Q^d_x = 100 – 5P_x = 100 – 5×9 = 55
and         Q^s_x = 10 + 5P_x = 10 + 5×9 = 55
⸫ Equilibrium price (P_x­) = 9 and equilibrium quantity (Q_x) = 55.

(c) New demand equation is

Q^d_x' = 200 – 5P_x
But the supply equation remains the same,
Q^s_x = 10 + 5P_x
For new equilibrium
Q^d_x' = Q^s_x
or, 200 – 5P_x = 10 + 5P_x
or, 10P_x = 190
⸫ P_x = 19
Putting P_x = 19 in new demand equation and supply equation,
Q^d_x' = 200 – 5P_x = 200 – 5×19 = 200 – 95 = 105
Q^s_x = 10 + 5P_x = 10 + 5×19 = 10 + 95 = 105

(d) When demand equation changes with supply being fixed, price increases from 9 to 19 and quantity increases from 55 to 105 at new equilibrium.

10. The market demand and supply functions are as:

Q^d_x = 2400 – 2P    and   Q^s_x = 8P

On the basis of this information, answer the following questions.

(i)     Determine the equilibrium price and quantity.

(ii) What is the effect of tax Rs. 40 per unit on production?

Solution:

(i) Given, Q^d_x = 2400 – 2P    and   Q^s_x = 8P

For market equilibrium: Q^d_x =  Q^s_x

or, 2400 – 2P = 8P

⸫ P = 240

Putting the value of P in demand and supply functions:

Q^d_x = 2400 – 2P = 2400 – 2×240 = 1920

and   Q^s_x = 8P = 8×240 = 1920

Hence, equilibrium price is Rs. 240 and equilibrium quantity is 1920 units.

(ii) If the government imposes tax on production at a rate of Rs. 40 per unit on production, the new supply function will be,

Q^s_x' = 8(P – 40) = 8P – 320 but the demand function will remain same.

For market equilibrium,

Q^d_x = Q^s_x'

or, 2400 – 2P = 8P – 320

or 10P = 2720

⸫ P = 272

Putting the value of P in demand and supply function,

Q^d_x = 2400 – 2P = 2400 - 2×272 = 2400 – 544 = 1856

Q^s_x' = 8P – 320 = 8×272 – 320 = 2176 – 320 = 1856

Hence, equilibrium price is Rs. 272 and equilibrium quantity is 1856.

11. The individual demand function is given as P_x = 0.2Q^d_x – 30 and individual supply function is Q^s_x = 20P_x, where symbols have their usual meaning. If there are 100 identical consumers and 100 identical suppliers in the market for a particular commodity x, obtain,

(a)    Individual demand and supply schedules

(b)    Market demand and supply functions

(c)    Equilibrium price and quantity

(d)    Equilibrium price and quantity, mathematically.

Solution:

Demand function is, P_x = 0.2Q^d_x – 30 
                        or, 0.2Q^d_x  = 30 + P_x 
                        or, Q^d_x = 150 + 5P_x

(a) Individual demand and supply schedule

Price	DF: Qdx = 150 + 5Px	SF: Qsx = 20Px
8 9 10 11 12	150 + 5 × 8   = 190 150 + 5 × 9   = 195 150 + 5 × 10 = 200 150 + 5 × 11 = 205 150 + 5 × 12 = 210	160 180 200 220 240

(b) Since, there are 100 identical consumers. So, the market demand function = 100Q^d_x

Q^d_x' = 100(150 + 5P_x)
Q^d_x' = 15000 + 500P_x
Since, there are 100 identical suppliers. So, the market supply function = 100Q^s_x
Q^s_x' = 100(20P_x)
Q^s_x' = 2000P_x

(c) Market demand and supply schedule

Price	MDF: Qdx' = 15000 + 500Px	MSF: Qsx = 2000Px
8 9 10 11 12	15000 + 500 × 8   = 19000          19500 20000 20500 21000	16000 18000 20000 22000 24000

From the above market demand and supply schedule, it is seen that at price (P_x) = Rs. 10, quantity demanded is equal to quantity supplied.

Hence, Equilibrium price (P_­x) = Rs. 100 and
Equilibrium quantity (Q^d_x­) = 20000 units

(d) For market equilibrium,

Q^d_x' = Q^s_x'
or, 15000 + 500P_x = 2000P_x
or, 1500P_x = 15000
⸫ P_x = 10
Putting the value of P_x is demand and supply function,
Q^d_x' = 15000 + 500P_x = 15000 + 500×10 = 20000
Q^s_x' = 2000P_x = 2000×10 = 20000
Hence, the equilibrium market price (P_x) = Rs. 10 and equilibrium market quantity (Q_x) = 20000 units

12. The market for pizza has the following demand and supply schedule.

Px (in Rs.)	Qdx (in units)	Qsx (in units)
50 60 70 80 90	150 125 100 75 50	50 75 100 125 150

(a) Graph the demand and supply curves. What is the equilibrium price and quantity in this market?

(b) If the actual price in this market were above the equilibrium price, what would derive the market toward the equilibrium?

(c) If the actual price in this market were below the equilibrium price, what would derive the market toward the equilibrium?

(d) If the quantity demanded at each price increased by 50 units, what would be the new equilibrium price and quantity? Show new equilibrium price and quantity in the graph.

Solution:

(a) Plotting the values of given schedule, we derive the demand curve and supply curve represented by DD and SS respectively in the graph.

On the basis of schedule and graph

Q^d_x = Q^s_x = 100 at P_x = 70

Hence, Equilibrium Price (P_x) = Rs. 70 and

        Equilibrium Quantity (Q_x) = 70 units

(b) If the actual price in the market were above the equilibrium, excess supply or surplus (Q^s_x>Q^d_x) would derive the market towards the equilibrium through the reduction in actual price.

(c) If actual price in the market were below the equilibrium price, excess demand or shortage (Q^d_x>Q^s_x) would derive market towards the equilibrium through the increase in actual price.

(d) The new schedule can be presented below with the increased by 50 units at each price.

Px (in Rs.)	Qdx (in units)	Qsx (in units)
50 60 70 80 90	150 + 50 = 200 125 + 50 = 175 100 + 50 = 150 75   + 50 = 125 50   + 50 = 100	50 75 100 125 150

In this situation, the demand curve shifts to the right as D₁ D₁ with same supply curve SS. From the table, it is seen that when price (P_x) = 80, the quantity demanded = quantity supplied = 125 units. Hence, the new equilibrium price (P_x) = Rs. 80 and new equilibrium quantity (Q'_x) = 125 units. The same values are shown in the following graph:

13. The initial supply function is Q^S_x = – 40 + 20P_x. Suppose that as a result of an improvement in technology, the producer's new supply function becomes Q^S'_x = – 10 + 20P_x. Answer the following questions.

a. Derive the producer's supply schedules.

b. On the set of axes, draw this producer's supply curves before and after the improvement in technology.

c. How much of commodity X does this producer supply at the price of Rs. 4 before and after the improvement in technology.

Solution:

a. Producer's supply schedule

Price (in Rs.)	QSx = – 40 + 20Px	QS'x = – 10 + 20Px
6	80	110
5	60	90
4	40	70
3	20	50
2	0	30
1	-	10
0.5	-	0

b. Graphical plotting: 

c. Before the supply increased (shifted down), the producer offered for sale 40 units of X at the price of Rs. 4. After the improvement in technology, the producer is willing to offer 70 units of X at the same commodity price of Rs. 4.

14. A market consists of three consumers A, B and C whose individual demand functions are given below:

A: P = 35 – 0.5Q_A

B: P = 50 – 0.25Q_B

C: P = 40 – 2Q_C

The market supply is given by Q_S = 40 + 3.5P. Find,

(a)    Market demand for the commodity

(b)    Determine the equilibrium price and quantity

(c)    Determine the amount that will be purchased by each consumer.

Solution:

(a) Since demand is the function of price. Hence,

For A
P = 35 – 0.5Q_A
or, 0.5Q_A = 35 – P
⸫ Q_A = 70 – 2P is the demand function for consumer A.
For B,
P = 50 – 0.25Q_B
or, 0.25Q_B = 50 – P
⸫ Q_B = 200 – 4P is the demand function for consumer B.
For C,
P = 40 – 2Q_C
or, 2Q_C = 40 – P
⸫ Q_C = 20 – 0.5P is the demand function for consumer C.
We know that market demand is the sum of all consumers demand, thus,
M_D = Q_A + Q_B + Q_C
M_D = 70 – 2P + 200 – 4P + 20 – 0.5P
M_D = 290 – 6.5P is the market demand for the commodity.

(b) For equilibrium price and quantity (market equilibrium)

Q_D = Q_S
290 – 6.5P = 40 + 3.5P
or, – 6.5P – 3.5P = 40 – 290
or, –10P = – 250
⸫ P = 25
Substituting P = Rs. 25 in demand function,
Q_D = 290 – 6.5×25 = 290 – 162.5 = 127.5 units
Hence, the equilibrium price is Rs. 25 and equilibrium quantity is 127.5 units.

(c) Amount purchased by consumer A = 70 – 2×25 = 20 units

Amount purchased by consumer B = 200 – 4×25 = 100 units
Amount purchased by consumer C = 20 – 0.5×25 = 7.5 units

15. Suppose there are 1000 identical individual in the market for commodity x, each with a demand function given by Q^D_x = 12 – 2P_x and 100 identical producers of commodity x, each with a supply function given by Q^S_x  = 20P_x, then find;

i.  Market demand function (Q^D_x) and market supply function (Q^S_x) for commodity

ii. The equilibrium price and he equilibrium quantity.

Solution:

i. Market demand function = (12 – 2P_x)×1000 = 12000 – 2000P_X

again, the market supply function = (20P_x)×100 = 2000P_x

ii. Equilibrium price is when market demand = market supply

12000 – 2000P_X  = 2000P_x

or, P_x = Rs. 3

and equilibrium quantity (Q^S_x) = 2000×3 = 6000 units

16. Suppose the market demand for pen is given by Q^D = 400 – 4P and the market supply for pen is given by Q_S = -10 + 6P where, P = price per pen. In equilibrium, how many pens will be sold at what price?

Solution:

Given, Market demand (Q^D) = 400 – 4P

Market supply (Q^S) = -10 + 6P

For equilibrium, Market demand (Q^D) = Market supply (Q^S)

or 400 – 4P = -10 + 6P

or, 10P = 410

⸫ P = Rs.41

For equilibrium quantity

Q^D = 400 – 4×41 = 400 – 164 = 234 units

Q^S = – 10 + 6×41 = – 10 + 246 = 236 units

⸫ Q^D = Q^S

Hence, equilibrium price (P_x) = Rs. 41 and equilibrium quantity (Q_x) = 236 units.

17. Consider the following demand schedule:

Price (Rs./Kg.	Quantity (Kg./month)
	At Y = Rs. 5000	At Y = 10000	At Y =Rs. 15000
Rs. 10	3	5	7
Rs. 15	2	4	6
Rs. 20	1	3	5
Demand Curves	D1	D2	D3

Graph the above demand curves D₁, D₂ and D₃, and explain the concept of movement along a demand curve, and shift in demand curve.

Solution:

In the above diagram, there are three demand curves D₁, D₂ and D₃. At income Rs. 5,000, demand is decreasing from 3 units to 2 units to 1 units when price is increasing form Rs. 10 to Rs. 15 to Rs. 20. Same is the case for income Rs. 10,000 and 15,000. This is known as the decrease in quantity demanded or downward movement along a demand curve, contraction in demand.

On the other hand, at the same price Rs. 10, there is increase in demand from 3 units to 5 units and 5 units to 7 units. It is due to increase in income from Rs. 5,000 to Rs. 10,000. Same is the case at price Rs. 15 and Rs. 20. Since, there is increase in demand at the same price, the demand curve is shifting rightward from D₁ to D₂ and D₂ to D₃. This is known as increase in demand or rightward shift in demand curve.

18. From the following demand and supply function:

D = 30 – 3P and S = 20 + P

i. Equilibrium price and quantity

ii. Show the effect on demand and supply if price increased by Rs. 2

Solution:

i. Given, D = 30 – 3P and S = 20 + P

For market equilibrium,

D = S

or, 30 – 3P = 20 + P

or 4P = 10

⸫ P = 2.5

Now,

D = 30 – 3P = 30 - 3×2.5 = 22.5

S = 20 + P = 20 + 2.5 = 22.5

Equilibrium price (P) = 2.5 units and D = S = 22.5 units

ii. If price increases by Rs. 2, new price (P) will be equal to 4.5, then

D = 30 – 3P = 30 - 3×4.5 = 16.5

S = 20 + P = 20 + 4.5 = 24.5

Then, here will the situation D<S (excess supply or surplus). In other words supply will exceed demand by 24.5 – 16.5 = 8.